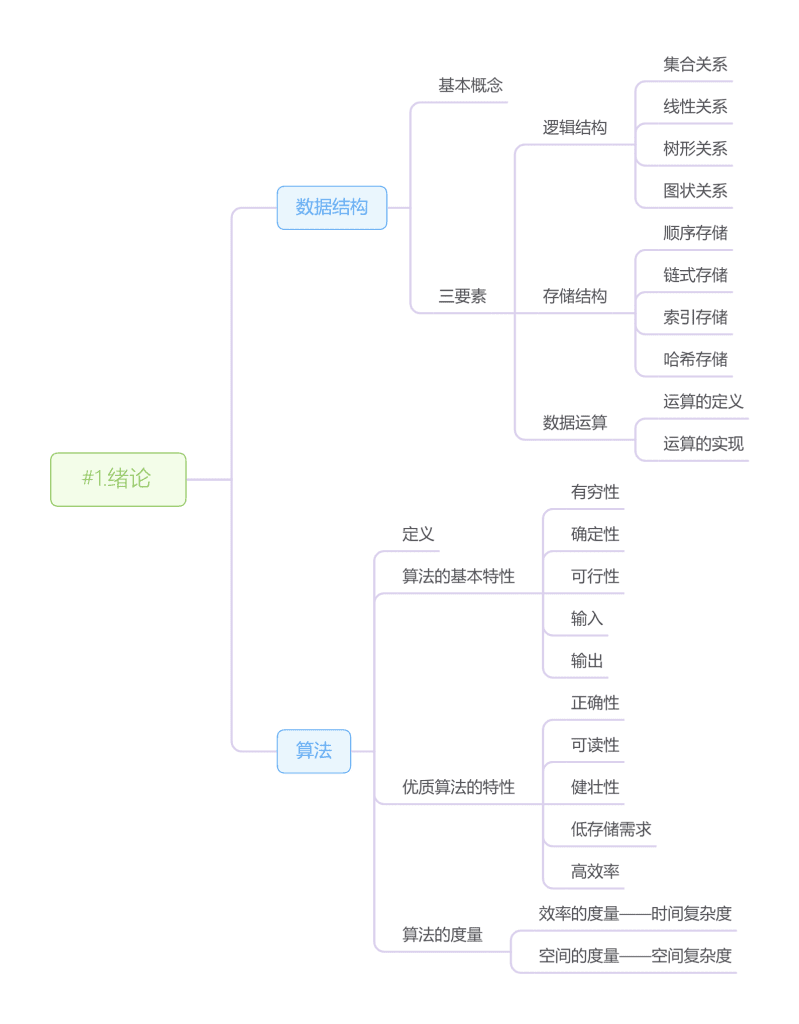
一、数据结构

（一）基本概念

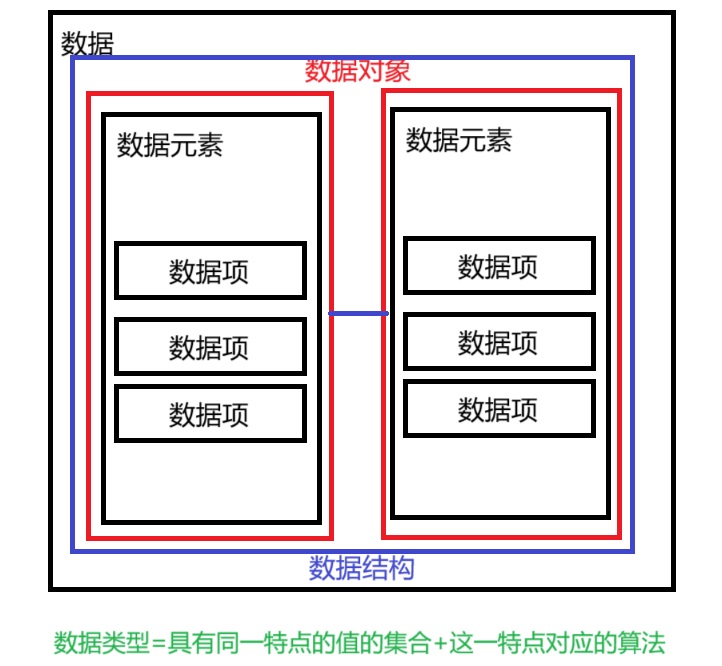
1、数据

数据是用于承载信息的一类载体，它以某种方式表示某一个信息。对于计算机而言，也就是二进制的0和1.

2、数据元素

数据元素是我们根据某个需求确定的数据的基本单位，在实现这个需求的过程中，通常将数据元素视为一个整体进行考虑。例如，在C中定义的struct结构体。

3、数据项

数据项是构成数据元素的不可分割的最小单位，它反应这个数据元素某个方面的信息。例如，在C的struct结构体中的组成部分。

4、数据对象

数据对象是指具有相同性质的数据元素的集合，强调的是某两个数据元素类型是相同的。例如，在C中我们定义struct结构体，用此结构体作为数据类型声明的两个结构体A和B。

5、数据结构

数据结构是指数据元素之间的关系。例如，我们声明的A和B之间是线性关系，或者集合关系？

6、数据类型

数据类型是具有同一特点的值的集合以及这一特点对应的算法。例如，C中的int类型，既包含整型数，也包含整型数所对应的一些运算（加减等）。

（二）三要素

1、逻辑结构

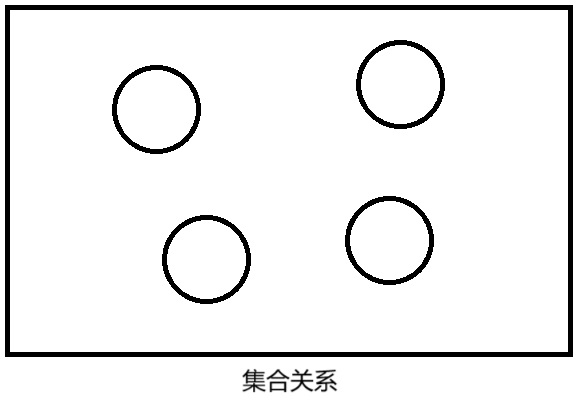
（1）集合关系

集合关系：数据元素同属于一个集合，除此之外没有其他关系。一个数据元素在逻辑上既没有前驱，也没有后继。

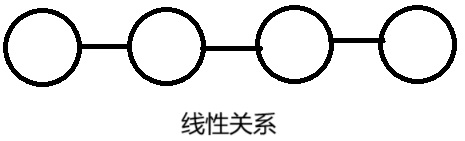
（2）线性关系

线性关系：数据元素之间是一对一的关系。一个数据元素在逻辑上至多有一个前驱，至多有一个后继。

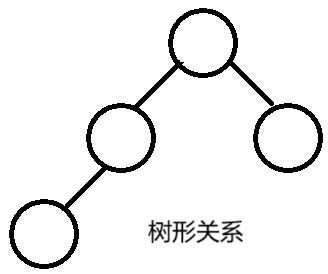
（3）树形关系

树形关系：数据元素之间是一对多的关系。一个数据元素在逻辑上至多有一个前驱，但可以有多个后继。

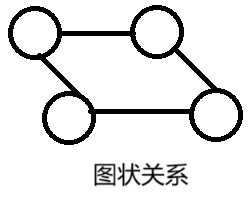
（4）图状关系

图状关系：数据元素之间是多对多的关系。一个数据元素在逻辑上可以有多个前驱，也可以有多个后继。

2、存储结构

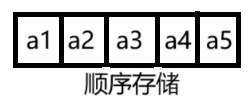
（1）顺序存储

顺序存储：把逻辑上相邻的数据元素，在物理位置上也相邻存储。

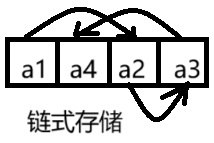
（2）链式存储

链式存储：把逻辑上相邻的数据元素，通过指针的方式连接起来，物理位置上可以不相邻。

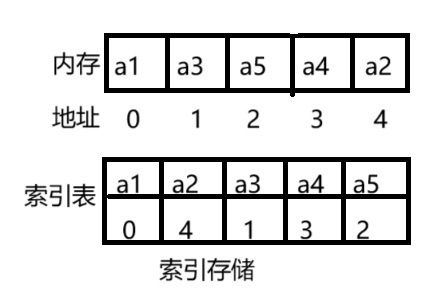
（3）索引存储

索引存储：通过建立索引表的方式记录数据元素在内存上的位置。

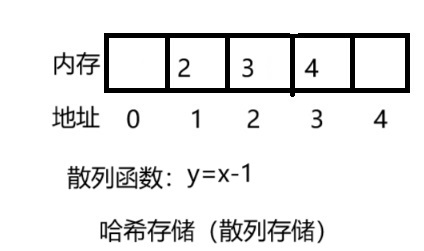
（4）哈希存储

哈希存储：又叫散列存储，通过散列函数将数据元素的值映射到对应的内存地址上。

3、数据运算

（1）运算的定义

数据运算的定义是针对逻辑结构的，也就是在逻辑上要实现什么效果。

（2）运算的实现

数据运算的实现是针对存储结构的，也就是在某种存储结构下，该如何实现定义的效果。

二、算法

（一）定义

算法是求解问题的步骤，也就是说对于某一个问题，我们会按照怎样的步骤去处理它。例如，数学中的函数y=f(x)，我们对于每一个问题x，会按照f定义的这种步骤去处理它，最终得到y。

（二）算法的基本特性

（1）有穷性

有穷性是指算法的步骤应该是有限的，它在执行有穷步之后应该结束；同时，它所消耗的时间也应当是有限的。例如，y=f(x)，我们的目的是得到y，所以f不能是算不完的。

（2）确定性

确定性是指算法的步骤应当是无歧义的，对于相同的输入会得到相同的输出。例如，y=f(x)，我们的目的是得到y，所以f定义的步骤应该是确定的，不能对于同一个x，得到不同的y。

（3）可行性

可行性是指算法的每一步应当是可以实现的，在计算机中，也就是指算法可以通过有限次基本运算来实现。例如，y=f(x)，我们的目的是得到y，那么f定义的步骤应当是可以计算的。

（4）输入

算法应当有0个或多个输入。例如，y=1，没有输入；y=f(a,b,c)，有多个输入。

（5）输出

算法应当有1个或多个输出。例如，y=f(x),x=g(u),u=h(v),总体来看，y=f{g[h(v)]}，但我们可以把得到的y=f(x),x=g(u),u=h(v)都输出出来。

（三）优质算法的特性

（1）正确性

正确性指的是优质算法应当能够正确地解决问题。例如，若我们知道x=1时y=2，对于函数y=f(x)=x+2来说，它虽然算出了一个y值，但不正确。

（2）可读性

可读性指的是优质算法应当便于人们去理解。

（3）健壮性

健壮性指的是优质算法应当对非法的输入有适当的反应或者处理。例如，y=f(x)=1/x，当输入为x=0时，我们会发现这一函数无法计算，所以我们可以特别定义当x=0时，函数无意义。

（4）低存储需求

低存储需求是指算法占用的内存空间小，表现为低空间复杂度。

（5）高效率

高效率是指算法消耗的时间少，表现为低时间复杂度。

（四）算法的度量

（1）时间复杂度

度量算法的时间复杂度T(n)，我们通常是分析某一个操作在算法中重复的次数和问题规模n之间的关系，通常表示为n的函数，只保留最高次，忽略低次项和最高次项的系数。

一般来说，一个算法在不同的情况下会有最好时间复杂度、平均时间复杂度、最坏时间复杂度。

（2）空间复杂度

度量算法的空间复杂度S(n)，我们通常是分析存储空间的大小和问题规模n之间的关系，通常表示为n的函数，只保留最高次，忽略低次项和最高次项的系数。